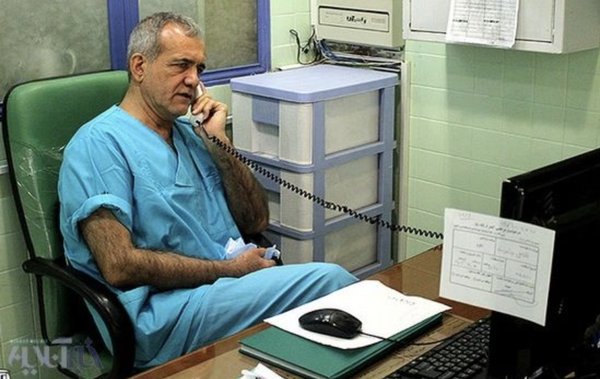
تحلیل نتایج انتخابات براساس قانون بنفورد چقدر اعتبار دارد؟
پس از اعلام نتایج انتخابات، چندین حساب کاربری در شبکههای اجتماعی براساس «قانون بنفورد» ادعا کردند که نتایج اعلام شده، عددسازی است. مشهورترین آنها، ویدیویی بود که کاوه مظفری در اینستاگرام منتشر کرد:
کاوه مظفری، پزشک و اینفلوئنسر سلامت در اینستاگرام، ساکن تورنتو است که در زمینه آموزش ریاضی نیز فعال است. این ویدیو در روزهای گذشته در شبکههای اجتماعی مختلف دستبهدست شد و بهعنوان شاهدی بر عددسازی در نتایج انتخابات چهاردهمین دوره ریاست جمهوری اسلامی ایران استفاده شد. (یک نمونه طولانی).
غیر از او، سیامک جوادی، مدرس و پژوهشگر اقتصاد مالی در دانشگاه تگزاس نیز در رشتهتوییتی که بازخورد زیادی داشت، به قانون بنفورد اشاره کرده بود. آقای جوادی بعدا این توییت خود را حذف کرد و رشته توییت زیر را برای اطلاعات تکمیلی منتشر کرد. ایراد محاسبه آقای جوادی هم این بود که قانون بنفورد را برای اعداد نرخ مشارکت حساب کرده بود که بازه متناهی نیستند و شامل این قانون نمیشود.
در این پست سعی میکنم به نقدهایی که در خصوص استفاده از نرخ مشارکت شد، پاسخ بدم.
— سیامک جوادی | Siamak Javadi (@SiamakJavadi) July 2, 2024
ایراد درست و منطقی که به محاسبات گرفته شده اینه که از درصد مشارکت برای تست قانون بنفورد نباید استفاده کرد. چونکه نرخ مشارکت بصورت خوشهای و در یک بازهای محدود که به اندازه کافی بزرگ نیست متمرکز هست. https://t.co/tuueKOs6P3
قانون بنفورد چیست و چه میگوید؟
قانون «بنفورد» که در انتخابات ۱۳۸۸ با مقاله «بودوین اف. روکما» فیزیکدان فرانسوی در ایران شهرت پیدا کرد، میگوید اگر عددی بهصورت طبیعی بهدست آمده (حاصل عدد سازی نیست) آن وقت احتمال اینکه اولین رقم سمت چپ آن ۱ باشد ۳۰/۱ درصد است، احتمال اینکه اولین رقم سمت چپ ۲ باشد ۱۷/۶ درصد است و الی آخر.
این قانون برای بسیاری از دادهها برقرار است، مثلا در صورتحسابهای برق، شماره خیابانها، قیمت سهام، مقدار جمعیت، آمار مرگ و میر، طول رودخانهها، ثابتهای فیزیک و ریاضیات.
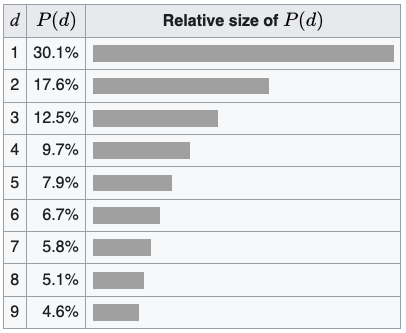
احتمالات قانون بنفورد برای اعداد در مبنای ده
یعنی اگر از مجموعهای از اعداد که طبیعی ساختهشدهاند، تعدادی عدد را انتخاب کنیم، از هر سهتای آنها، یکی با ۱ شروع میشود ولی از هر بیستتا یکی با ۹ شروع میشود.
قانون بنفورد BL را میتوان برای رقم دوم (۹۰ عدد) 2BL و حتی رقم سوم (۹۰۰ عدد) 3BL از سمت چپ عدد هم محاسبه کرد. در این صورت باز هم دقت محاسبه بیشتر و بیشتر میشود. در جستجو برای کشف تقلبهای مالیاتی، سراغ این حد از دقت میروند (نمونه۱، نمونه۲).
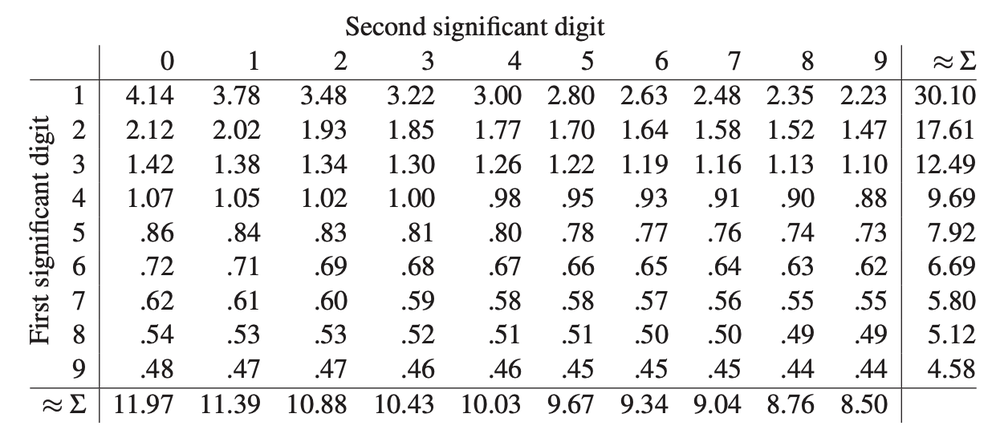
احتمالات قانون بنفورد برای ۲ رقم سمت چپ در مبنای ده
آیا تفاوت نتایج با قانون بنفورد نشانه عددسازی است؟
قضاوت در این مورد ساده نیست و به ماهیت دادهها و تعداد دادهها نیز بستگی دارد. اختلاف با قانون بنفورد به خودی خود بهمعنی «عددسازی» نیست؛ بلکه به معنی «مشکوک به عددسازی» است. یعنی وقتی دادههای مورد خاصی (مثلا مالیات) با قانون بنفورد نمیخورد، دادهها را زیر سوال نمیبرند بلکه روش و متدولوژی تولید دادهها را با دقت بیشتری بررسی میکنند.
مانند هر پدیده دیگری که سرشت آماری دارد، در اینجا نیز با مجموعه وسیعی از حالتهای مختلف مواجه هستیم. ممکن است احتمال وقوع پدیدهای بسیار بسیار پایین باشد، اما رخ دهد. بنابراین قانون بنفورد درباره احتمال عددسازی صحبت میکند و اثباتی بر عددسازی نیست. حتی مواردی کاملا مخالف نیز وجود دارد.
در مورد کاربرد قانون بنفورد در انتخابات هم شواهدی وجود دارد که نشان میدهد این قانون مفید است (والتر مبین، ۲۰۰۶) و مطالعاتی هم نشان میدهد که چندان هم فایدهای نداشته، یعنی به اشتباه دادههایی که درست بوده را مشکوک اعلام کردهاست (نتایج یک تحقیق پایاننامه دانشجویی).
با وجود اینکه بیش از یک قرن از سابقه کشف قانون بنفورد میگذرد اما این قانون را تازه «تئودور هیل» استاد دانشگاه جورجیا تک، در سال ۱۹۹۸ توانست ثابت کند. سال ۲۰۲۰ که ادعای مشابهی در انتخابات ریاست جمهوری ایالات متحده مطرح شد (ادعای عدم همخوانی صندوقهای میلواکی با قانون بنفورد) خبرگزاری رویترز، در راستیآزمایی به سراغ تئودور هیل رفت و از او پرسید: «آیا با قانون بنفورد میتوان فهمید در انتخابات تقلب شده؟» تئودور هیل، کاشف اثبات قانون بنفورد در پاسخ ایمیلی گفت:
اول، من میخواهم تاکید کنم که قانون بنفورد نمیتواند برای «اثبات تقلب» استفاده شود. این فقط یک تست «زنگ خطر» (Red Flag) است که میتواند شک و تردیدهایی را ایجاد کند. مثلا IRS (اداره خدمات درآمد داخلی - مالیات آمریکا) چند دهه است که از تست بنفورد برای شناسایی کلاهبرداران استفاده میکند، اما تنها برای تشخیص دادههای ورودی مشکوک از آن استفاده میشود و سپس محققان به سراغ آن هدف میروند و به دنبال شواهد میگردند. اینکه یک مجموعه داده از BL پیروی میکند یا نمیکند، دلیل هیچچیز نمیشود.
والتر مبین (Walter Mebane) هم در مقاله سال ۲۰۰۶ خود که بر قانون بنفورد برای دو رقم (2BL) تمرکز کردهبود مینویسد:
در هر صورت، آزمون 2BL به تنهایی نباید دلیلی بر وقوع تقلب یا پاکبودن یک انتخابات تلقی شود. اختلاف زیاد در تست 2BL میتواند ناشی از عوارضی غیر از تقلب نیز باشد. برخی از انواع تقلبها هم هستند که با تست 2BL نمیتوان آنها را کشف کرد.
سال ۲۰۲۰، بعد از انتخابات، افراد زیادی از مبین خواستند انتخابات میلواکی را بررسی کند، او در گزارشی نوشت:
«اولین ارقام شمارش آرای حوزهها برای تلاش برای تشخیص تقلب در انتخابات مفید نیست.»
تفاوت دادههای انتخابات ۱۴۰۳ با پیشبینی بنفورد چقدر است؟
فکتنامه این موضوع را جداگانه بررسی کرد که آیا نتایج انتخابات ریاست جمهوری از چنین الگویی تبعیت میکند یا نه. برای این منظور دادههای دور اول انتخابات ۱۴۰۳ را برای کاندیداها و آرای باطله، به تفکیک استانی بررسی کردیم (منبع ستاد انتخابات وزارت کشور) که نتایج را در زیر میبینید:
این انحراف چه معنایی دارد؟
با استفاده از انواع روشهای محاسبه خطا میتوان انحراف دادهها از قانون بنفورد را بهدست آورد و با مقایسه آن با تعداد دادهها، به معیاری برای «مشکوک به عددسازی بودن دادهها» پیبرد اما هیجکدام دلیل مستقیمی بر عددسازی نیست.
تحلیل براساس قانون بنفورد وقتی دقیقتر میشود که تعداد نمونهها بیشتر شود. مثلا بررسی آرا هر دو دوره به تفکیک شهرستان، یا به تفکیک صندوق، کمک بیشتری میکند که بتوان فهمید چقدر انحراف از قانون بنفورد وجود دارد.
اما به هر حال باید توجه کرد که انحراف از قانون بنفورد، مانند هر پدیده آماری دیگری، تنها یک نشانگر است که «مشکوکبودن به عددسازی» را تقویت میکند و اثباتکننده «عددسازی» نیست.